2025. 2. 24. 17:53ㆍ수리통계학
안녕하세요. 월요일 오후입니다.
이젠 대학생의 방학도 얼마 남지 않았군요. 아직 날씨가 쌀쌀한데 말이죠.
.
.
할 얘기가 많아서 서론없이 바로 들어가보도록 할께요.
오늘은 포아송 분포로 들어갑니다. 사실 제가 제일 좋아하는 분포입니다.
조건이 까다롭긴 하지만, 다른 확률분포들보다는 활용성이 좋아서입니다.
시간이나 공간을 표현할 수 있다는 것이 흥미롭기도 하고요.
사실 이항분포 다음에 기하분포나 음이항분포를 다루어야 하지만,
이항분포 공식의 단순 응용인데다, 향후 나오는 내용들과 직접적으로 연결되는 부분이 없어
곧장 포아송 분포로 건너뛰었습니다.
다시 말하면, 포아송 분포는 자체적인 활용성뿐 아니라 나중에 나오는 내용들과도 밀접한 관계가 있는 파트라는 의미겠죠?
약간 스포를 하자면,
이항분포 → 포아송 분포 → 감마분포 → (정규분포, 카이제곱분포, t분포 등등)
이렇게 연결성이 깊습니다.
흥미로운가요? 그럼 슬슬 시작해보도록 합시다.
[포아송 분포란 무엇인가]
먼저 포아송 분포를 유도해내기 전에,
포아송 분포가 무엇인지 감을 잡을 필요가 있다고 생각해요.
그래서 교재에 나와있는 사례들로 예시를 들어보도록 할께요.
● 강이나 하천에서 일정한 "부피"의 물에 존재하는 부유생물의 "수"
● 일정한 "시간" 동안 컴퓨터 서버에 요청되는 접속 "횟수"
중요한 부분에 큰 따옴표를 해놨는데, 잘 보이시나요.
이해를 위해 이전에 다룬 이항분포로 예시를 들어보도록 할께요.
이항분포는,
"n번 시행에서 (1과 0 중) 1이 x번 뽑히는 경우"를 다룹니다.

두 수평선 그림 중 위쪽 놈이 일반적인 이항분포를 나타낸 결과일 거에요. k번째(k=1,2,...,n) 베르누이 시행 결과를 쭉 늘어뜨려놓으면 위와 같이 0이 나오는 경우, 1이 나오는 경우가 있을 겁니다.
그럼 이번에는 n 횟수를 조금 키워볼께요. (바로 아래 수평선 그림이 되겠죠?)
대신 그만큼 1이 뽑히는 확률(p)도 작아진다고 해볼께요. 그래서 1이 뽑히는 빈도는 예전과 비슷한데, 시행횟수 자체는 굉장히 많아진 그런 상황인 거죠.
수평선이 조금 더 촘촘해졌죠.
하지만 아직 부족합니다.
이젠 n을 무한대(∞)로 보내볼께요. 그럼 수평선이 "빈틈없이 빼곡하게" 채워질 거에요.
그럼 우리는 이것을 '시간'이나 '공간'처럼, 빈 공간이 없는 연속 개체로 취급할 수 있게 될 겁니다.
'시간'으로 본다면(그게 우리가 이해하기 조금 더 편하니까),
수평선은 이제 하나의 타임라인으로 볼 수 있겠네요.
앞선 예시들을 다시 확인해볼까요?
● 강이나 하천에서 일정한 "부피"의 물에 존재하는 부유생물의 "수"
● 일정한 "시간" 동안 컴퓨터 서버에 요청되는 접속 "횟수"
빈틈없이 빼곡히 채워진 "물" 안에 부유생물의 "수" (부유생물 나오면 1, 그냥 없으면 0)
빈틈없이 빼곡히 채워진 "시간" 동안 서버 접속요청 "횟수" (요청 있으면 1, 아닌 시간에는 0)
어떤 걸 확인할 수 있나요?
① 대부분의 공간을 채우고 있는 0.
② 아주 특별한 이벤트가 되어버린 1.
.
.
좋습니다. 그럼 이 예시들을 구현할 구체적인 조건들을 확인해볼까요?
[포아송 과정 (Poisson Process)]
아래 4가지 조건들을 만족하면, 이를 포아송 분포로 활용할 수 있습니다.
하나씩 살펴볼께요.
① 정상성, Stationarity
무슨 말일까요? 당연히 비정상이면 안 될 것 같긴 합니다. (죄송합니다. 농담입니다.)
저도 찾아봤는데, 한자 뜻을 보면
定常性
이렇게 됩니다.
네, 아직도 무슨 말인지 모르겠죠.
가운데 있는 글자가 '항상 상'입니다. 그래서
무엇인가가 '항상' 일정하다
이 정도로 감을 잡고 내용을 확인해볼께요.
'정상성'
: 현상이 발생하는 횟수의 분포는 시작하는 시각에 관계없다.
즉, Nt의 분포와 N(s+t)-Ns의 분포가 같고, N0=0이다.
여기서 Nt는 't 시간이 흐를 때, 발생한 횟수'를 말합니다. N을 볼 때 Number(횟수)라고 떠올리면 되겠네요.
그래서
't 시간 동안 발생한 횟수 분포랑 s 시점부터 s+t 시점까지 발생한 횟수 분포에 차이가 없다'
그런 말이 되겠죠. 결국 지속시간은 t로 같으니까요.
결국 시작점이 다른 건데(0 vs s) 이것 때문에 확률이 달라지지 않는다는 것이죠.
.
.
예시를 들어볼까요.
아까 하천 물 속의 부유 생물 수에 대해 다시 이야기해봅시다.
여기 웅덩이가 있을 때,
제가 여기서 한 컵 물을 뜨거나
아니면 몇 발자국 옆으로 움직여서 한 컵 샘플을 채취하나
그 안에 들어있는 부유 생물 수에는 큰 차이가 없어야 한다는 겁니다. (포아송 분포를 사용해서 이 확률을 계산하고 싶다면)
그런데 하천 속 부유 생물 수는 적절한 활용사례가 될 수 있을 것 같은 게,
실제로 물 속에서 특정 구간에만 부유 생물들이 몰려 있을 것 같진 않단 말이죠. (전문가분들 연락주세요.)
물 속에 고르게 퍼져있을 것 같고, 그래서 어디서 샘플을 채취하나 큰 차이가 없을 것 같습니다.
② 독립증분성, Independent increment
두 번째입니다.
시각 0부터 t까지 현상이 발생하는 횟수와
시각 t부터 t+h(h>0)까지 발생하는 횟수는
서로 독립이다.
서로 발생확률에 영향을 미치지 못한다는 것이겠죠.
독립성이 보장된다는 것입니다.
③ 비례성, Proportionality
짧은 시간 동안에 현상이 한번 발생할 확률은 시간에 비례한다.
수식으로 한 번 확인해볼까요?
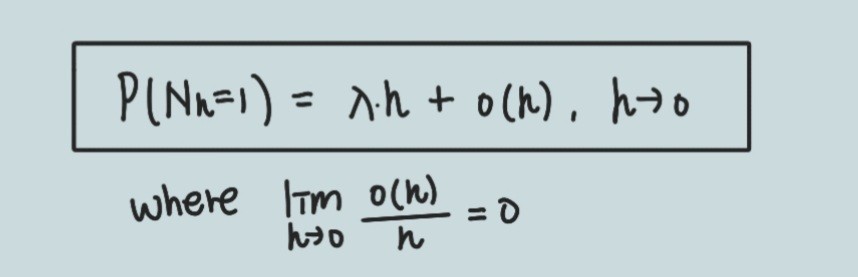
*여기서 o(h)는 'small-o notation'으로 일종의 오차항이라고 보면 될 것 같습니다. 정의는 그림 아래쪽에 나와있지만, 자세한 맥락은 이후 설명에서 해보도록 하지요.
P(Nh=1)에서 Nh는 'h 시간 동안 발생한 횟수'를 말합니다.
그래서 이는 'h 시간 동안 1번 발생할 확률'을 의미하겠습니다.
이 확률을 어떻게 계산할까 생각해보니,
λ(람다)는 "단위시간 당 평균 발생횟수"를 의미합니다.
이런 단위시간은 또 뭘까요?
기준 시간 정도로 이해하면 되겠습니다. 우리가 자연수를 센다고 하면 한 단위는 1이 됩니다.
반면 우리가 여기에 2를 곱해서 2,4,6,8,... 이런 집합을 만들었다면 한 단위는 2가 되겠네요.
그렇기에 우리가 '특정한 단위시간'을 정해서 평균 발생횟수를 측정해보았더니, λ가 되더라
이렇게 보면 될 것 같습니다.
'단위시간' 당 횟수이기 때문에,
'h시간' 당 횟수는
단위시간 당 횟수에 h를 곱해주면 되겠네요.
그래서 λh가 나왔습니다.
그런데 이건 '평균' 값이죠.
위에서 정상성을 살펴보면서,
포아송 분포는 기본적으로 'even'하게 퍼져있는 상황을 상정한다는 느낌을 받으셨을지 모르겠습니다.
따라서 기본적으로 λ 하나의 모수(parameter)에 의해 확률이 계산될 만큼 평균의 힘이 강력하지만(나중에 수식을 보시면 아하 하실 수 있으실 거에요)
그럼에도 항상 상황에 따라, 당연히 어쩔 때는 더 발생하고 어떤 때는 덜 발생하고
그러겠죠.
그래서 o(h)라는 오차항을 넣어주었다고 생각하면 될 것 같습니다.
정의에서 '짧은 시간'이라고 했으므로, h→0으로 세팅한 것도 확인할 수 있군요.
마지막입니다!
④ 희귀성, Rareness
짧은 시간 동안에 현상이 두 번 이상 발생할 확률은 매우 작다.
아까 위에서 수평선을 빼곡히 채우는 예시를 들면서 결론으로
'1이 발생하는 경우는 아주 특별한 이벤트가 되어버린다'
이렇게 이야기했었습니다. n번 뽑을 때나, 무한번 뽑을 때나 1이 뽑히는 횟수가 비슷하면
상대적으로 무한번 뽑을 때 1이 뽑히는 확률이 극단적으로 작아지겠네요.
(베르누이 시행의 관점에서는 p가 작아질 겁니다.)
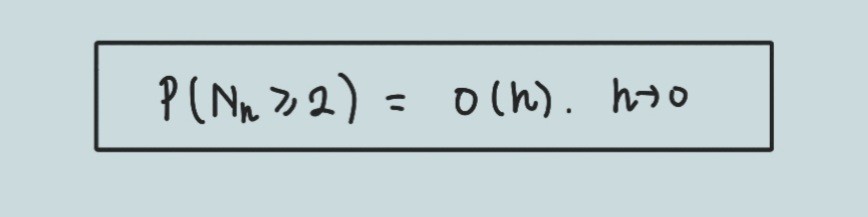
수식으론 위와 같이 적습니다. 즉, 이렇게 p가 작은데, 이게 연속으로 두 번씩이나 발생한다고요???
굉장히 희박할 겁니다.
p는 정말 희귀하게 발생하는 이벤트가 되어버렸으니까요.
좋습니다. 여기까지 포아송 과정을 모두 살펴봤습니다.
포아송 분포라는 흥미로운 분포를 활용하려면, 우리의 적용사례가 위 조건들을 만족하는지 꼼꼼히 확인해야 합니다.
그럼 다음 포스팅에서는 이 포아송 과정이 사실은 이항분포로 근사될 수 있다는 놀라운 사실을 다루도록 하겠습니다.
.
.
아름다운 느낌이 머물기를...
'수리통계학' 카테고리의 다른 글
| [수리통계학] 12. 포아송 분포 유도 (0) | 2025.02.25 |
|---|---|
| [수리통계학] 11. 이항확률의 포아송 근사 (0) | 2025.02.24 |
| [수리통계학] 9. 초기하 분포와 이항 분포의 관계 (0) | 2025.02.22 |
| [수리통계학] 8. 이항분포의 기댓값과 분산 계산 (0) | 2025.02.20 |
| [수리통계학] 7. 이항분포란 무엇인가 (1) | 2025.02.19 |