2025. 2. 25. 11:35ㆍ수리통계학
안녕하세요. 요즘은 매일같이 블로그를 쓰고 있어서 근황 토크도 없네요. (하하)

자주 봐서 나쁠 건 없지요.
오늘은 앞서 두 포스팅에 걸쳐 진행했던
이항확률의 포아송 근사를 마무리하려고 합니다.
막판에는 그토록 찾아다녔던 포아송 분포의 확률 모형을 확인할 수 있겠군요.
그럼 시작해볼까요?
먼저 지난 시간에 포아송 과정의 4가지 조건들을 검토하며
n이 무한히 커질 때, 결국 전체 발생횟수를 의미하는 Nt가 이항분포에 근사 표현될 수 있다는 것을 확인했습니다.
그럼 오늘 유도 과정에서는
n→∞에서 이항분포를 변형하여 포아송 확률을 표현하는 것에 집중해보도록 해요.
전체적인 수식의 흐름은
n→∞이 부담스러우니, 이 n을 잘 다루는 방식으로
(그냥 보면 발산할 것 같이 무섭게 생겼으니까, 수렴하도록 형태를 바꾸어본다.)
진행해보도록 할께요.

(별표1)
: 일단 이항분포의 기댓값(E[X])은 np로 계산하고, 그 값을 ' λ'라고 놓겠습니다.
문자를 줄이기 위해
p= λ/n
이렇게 치환하여 계산하도록 하겠습니다.

(별표2)
: 그래서 p 자리에 이젠 λ/n이 들어가 있는 것을 확인할 수 있습니다.
이번에는 nCx를 분해해보도록 할께요.
아시다시피, 조합은 분모의 두 팩토리얼(x!, (n-x)!) 첫번째 수의 합(x, n-x)은
항상 분자 팩토리얼 첫번째 수(n)과 같습니다.
다시 생각해보면, n!에서 (n-x)!만큼을 약분해서 없애보면
남은 갯수(n, (n-1), (n-2), ..., (n-x+1))는 x개가 된다는 것을 알 수 있겠네요.
n에서 n-1만큼을 제거한 것이 되니까,
남아있는 갯수는 x가 되는 게 자연스럽습니다.
그럼 이제 λ/n 치환에 의해 만들어진 n^x와 x!의 자리를 바꾸도록 할께요.
(별표3)
: 고등학교 수학시간에 변수가 무한대로 갈 때, 분자와 분모의 최고차항의 계수로 값이 수렴했던 걸 기억하시나요?
아까 n(n-1)(n-1)· · ·(n-x+1)이 총 x개라는 것을 확인했고,
n^x는 n이 x개 있는 것이니,
위와 같이 분모 n을 하나씩 나누어서 분자와 대응시켜줄 수 있습니다.
앞에 n이 무한대로 간다고 말하고 있으니
최고차항과 그 계수를 보면 모두 같다는 것을 알 수 있네요.
그래서 이 부분은 나중에 n→∞을 적용할 때 1이 n개 만들어지게 될 것입니다.
.
.
휴, 까다로운 n을 처리할 방법이 생겨 기쁩니다.
그럼 이제 빨간 밑줄 부분에 있는 n을 처리하기 위해 움직여봅시다.
위 그림2에서 빨간 밑줄이 처진 부분만 따로 가져왔습니다.
이제 이 부분에 있는 n을 잘 처리해주면, n→∞ 상황이 더 이상 무섭지 않을 것입니다.
아래 두 그림이 있네요.
왼쪽이 우리 수식에 있는 부분입니다.
그런데 형태가 자연상수 e의 정의와 닮았습니다. 변형을 가해서 충분히 e의 형태로 만들 수 있을 것 같아요.


e 정의는 '1에 아주 작은 수를 더한 값을 무한히 제곱한다'는 의미를 내포하고 있습니다.
형태적으로는 1에 더해지는 값의 '역수' 형태로 지수가 올라가네요.
우리가 다룰 부분을 e의 형태로 표현해낼 수 있다면, 이 역시 n→∞ 상황에서 탈출할 수 있는 좋은 기회입니다.
(e가 n→∞를 먹어버린다고 생각하면 좋겠네요.)
그럼 우리도 e의 형태를 따라, 우리의 식을 변형해보도록 합시다.

n→∞ (λ/n) = 0
이렇게 되니,
n→∞ (1- λ/n)^{-x} = 0
이 부분은 1^{-x}만 남게 되어, 결국 1이 되겠네요.
그럼 이제 원래 식으로 돌아와 봅시다.
n의 영향력을 없애기 위해 우리는 2가지 방법을 동원했습니다.
● 분모-분자 최고차항 맞추기
● 자연상수 e를 활용하기
이런 방법을 사용해 결국 n의 영향력을 모두 없애는 데 성공했습니다.
그리고 최종식을 얻게 되었네요.
감격스러운 순간입니다.
포아송 과정의 조건에서 출발하여, (포스팅 10)
그 개념들이 이항분포로 근사 표현될 수 있다는 것을 확인하고, (포스팅 11)
실제로 이항확률을 활용해 포아송 확률을 표현하는 데 이르렀습니다. (포스팅 12)

좋아요, 이제 포아송 분포를 알았으니 감마분포를 유도해낼 수 있고
감마분포를 알면
그 유명한 카이제곱 분포, 정규분포, t 분포 등을 표현해낼 수 있습니다.
좋은 과정이었던 것 같아요.
다음 시간에 또 됩도록 하겠습니다.
.
.
.
※ ※ 포아송 확률을 암기하는 팁
분자를 외울 때 헷갈릴 수 있습니다. 따라서 지수에 있는 λ가 그 다음으로 떨어진다고 생각하면 외우기 쉽습니다.
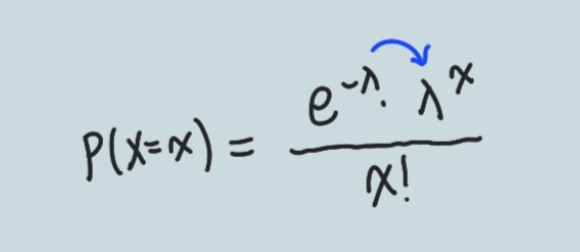
'수리통계학' 카테고리의 다른 글
| [수리통계학] 14. 지수함수의 기댓값과 분산 (3) | 2025.02.27 |
|---|---|
| [수리통계학] 13. 포아송에서 '단위 시간'의 의미와 지수분포 (0) | 2025.02.26 |
| [수리통계학] 11. 이항확률의 포아송 근사 (0) | 2025.02.24 |
| [수리통계학] 10. 포아송 분포와 포아송 과정(Poisson Process) (0) | 2025.02.24 |
| [수리통계학] 9. 초기하 분포와 이항 분포의 관계 (0) | 2025.02.22 |