2025. 2. 20. 00:25ㆍ수리통계학

안녕하세요. 머리가 지끈거리는 상태입니다. 아주 반가워요.
요즘 들어 뼈져리게 느끼는 한 가지가,
하루에 사용할 수 있는 에너지는 한정적이라는 것입니다.
쓸모없는 곳에 에너지를 많이 소비하면 그만큼 중요한 순간에 사용할 힘이 없어지게 되는 것 같아요.
예를 들면 약속시간에 늦을까 스트레스 받으며 지하철을 기다린다던지,
쉬는 시간을 두지 않고 몇시간에 걸쳐 어떤 활동들을 한다던지 등등
우선순위를 명확히 파악하고, 그에 따라 나머지 자극들을 포기할 수 있는 용기와 결단력이 필요합니다.
쉬운 일이 아니죠.
오늘은 다행히 어젯밤에 정리해둔 필기가 있어서, 따로 필기를 하진 않아도 될 것 같아요.
바로 시작해볼까요?
이항분포의 기댓값과 분산을 구해보도록 하겠습니다.
전체적인 전략은 이전 초기하 분포에서 다뤘던 것과 같습니다.
(이산변수이니 합의 기호를 사용해)
기댓값 정의를 따라 E(X)를 먼저 구합니다.
그 다음, E[X(X-1)]을 구해 분산 공식을 만들 겁니다.
기본적으로 식을 전개하는 아이디어도 초기하 분포 때와 많이 닮아,
이전 포스팅을 다시 한번 참고하시는 것도 좋은 생각일 것 같습니다!
이미 한번 경험한 과정이기 때문에, 두 이미지를 한 번에 배치하도록 할께요!


왼쪽 그림부터 보시죠.
(별표1)
: 시작하기에 앞서 가장 중요한 작업이 바로 sum(시그마)에서 x=0를 x=1로 바꾸는 것입니다.
기댓값은 앞에 변수 'X'가 곱해져 있으므로, x=0인 상황에서는 0이 됩니다.
따라서 ∑ 를 x=0부터 시작하던, x=1부터 시작하던 전체 값에는 변함이 없습니다.
어떻게 두어도 상관이 없다는 말이지만, 일단 우리는 뒤에 의도하는 바가 있으니 x=1부터 시작하는 것으로 바꾸어 둘께요.
이외에 combination에서 1/x를 빌려와 변수 X를 없애주는 것은 초기하 분포 때와 같은 아이디어입니다.
(별표2)
: X를 지우느라, n/x를 combination으로부터 꺼내게 되어, (n-1)C(x-1)이 되었습니다.
마치 애초에 n개가 아닌, n-1개를 뽑으려 했다고 거짓말을 하고 싶은 욕구가 생기는군요.
거짓말을 해봅시다.
지금 뒤에 p^{x}*(1-p)^{n-x}는 앞에 X를 지우느라 한개를 까먹은 걸 반영 못해서 둘이 아직 n개입니다.
그래서 p^{x}에서 p 하나를 빼봅니다.
그림을 보면 뒤에 P 하나가 나온 것을 확인할 수 있죠. 이렇게 하나를 빼돌렸더니, 이제 앞 combination과 같이 p와 (1-p)의 갯수가 합쳐서 n-1개가 됩니다.
완벽 범죄를 할 수 있을 것 같습니다.
이때 우리가 앞서 (별표1)에서 ∑를 x=0부터가 아닌 x=1부터 시작한 것이 신의 한 수가 되네요!
X는 하나도 1이 뽑히지 않은 0부터, n개 모두 뽑힌 n까지( 0 ≤ X ≤ n )
총 n+1개의 가능성이 있습니다.
그럼 지금 애초에 n-1개만 뽑고 있다고 뻥을 치고 있으니까,
X의 가능성도 한 개 적은 n개만 되어야 합니다.
그래서 아까 굳이 x=0부터 시작하지 않고, x=1부터 시작한 것이 빛을 바라죠.
x=1부터 시작하면, X는 1부터 n까지로, 딱 n개의 가능성만 가지게 되니까요.
아다리가 잘 들어맞습니다~
그래서 결국은 확률의 모든 경우를 다 더한 것이니,
확률의 합은 1이 된다는 확률의 공리에 따라
뒷부분은 1이 됩니다.
이 설명이 만족스럽지 않은 분들은 이항정리 공식을 떠올려서 이해하시면 좋을 것 같아요.
(오른쪽 E[X(X-1)]을 구하는 과정은 같은 논리가 적용되니, 설명은 생략하도록 할께요)
(애초에 n-1개 뽑았다고 사기(?)치는 부분을 수식으로 이해하고 싶으신 분들을 위해 설명 그림 첨부해놓겠습니다.)

이렇게 위에서 구한 결과들을 가지고 마지막 분산을 완성해봅니다.
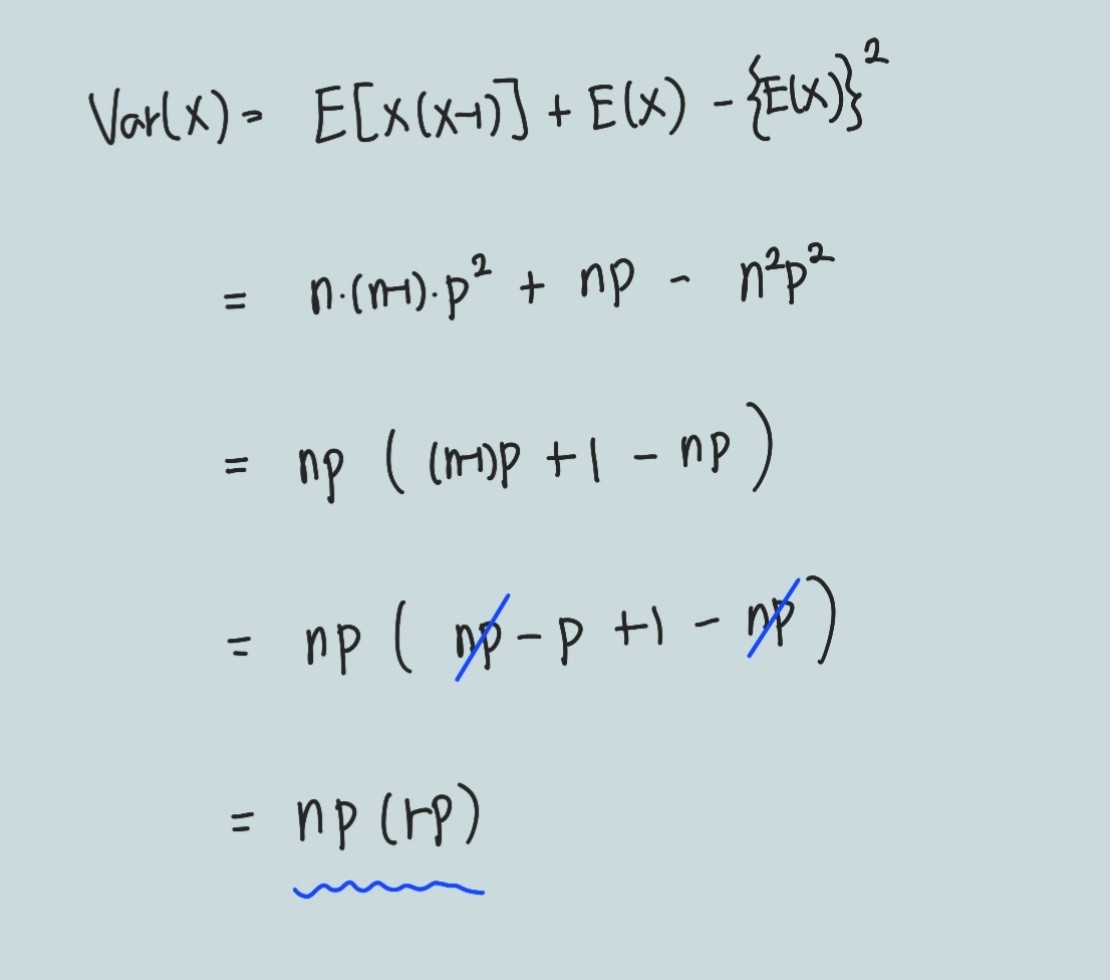
사실 이항분포의 평균과 분산을 정의를 사용해 수식으로 유도해보았지만,
np, np(1-p)를 보면 알 수 있듯,
그냥 베르누이 시행의 평균과 분산(p, p(1-p))를 n번씩 중첩해놓은 것입니다.
이는 이항분포가 '독립적인' 베르누이 시행의 반복으로 만들어졌기 때문이죠.
서로 영향을 주지 않으니 첫 시행, 두 번째 시행, ... , 마지막 시행까지 모두 기댓값이 p이고
앞서 미시 기댓값들을 합쳐 거시 기댓값을 구성했던 것처럼
이들이 n번 반복되니, np가 된 것입니다.
좋습니다. 다음 시간에는
① 이항분포의 구성물이었던
베르누이 시행으로 초기하 분포를 유도할 수 있다는 것을 확인해보고,
② 초기하 분포는 비복원 추출이고, 이항분포는 복원추출인데,
왜 n값이 커지면, 두 추출 방법 사이에 차이가 무시해도 될 정도로 작아지는지 이야기해보도록 하겠습니다.
최선이었던 하루가 되었길 바랍니다.
.
.
.
아름다운 느낌이 머물기를...
'수리통계학' 카테고리의 다른 글
| [수리통계학] 10. 포아송 분포와 포아송 과정(Poisson Process) (0) | 2025.02.24 |
|---|---|
| [수리통계학] 9. 초기하 분포와 이항 분포의 관계 (0) | 2025.02.22 |
| [수리통계학] 7. 이항분포란 무엇인가 (1) | 2025.02.19 |
| [수리통계학] 6. E[X(X-1)]의 해석과 초기하 분포의 분산 (1) | 2025.02.17 |
| [수리통계학] 5. 초기하 분포와 기댓값에 대한 생각 (0) | 2025.02.08 |