2025. 2. 22. 01:48ㆍ수리통계학
안녕하세요. 오늘도 인사드립니다.
잘 지내고 계신지요?
오늘은 금요일인데, 사정이 생겨 밖에 나가지 않았습니다. 덕분에 간만에 좀 편안한 하루를 보냈네요.

오늘은 제가 어떤 주제를 가지고 왔을까요?
자, 굉장히 궁금하죠?
(박수 한번 주세요~!)
죄송합니다. 평소대로 진행하죠.
저번 시간까지 우리는 초기하 분포를 마치고, 이항분포까지 살펴봤습니다.
그래서 오늘은 초기하 분포와 이항 분포의 관계에 대해 다루어보려고 합니다.
정확히는,
이항분포로 초기하 분포를 유도해보려고 합니다.
비복원 추출과 복원추출, 비독립성과 독립성
이렇게 상반되는 성질을 가지고 있는 두 분포인 것 같은데,
어떻게 이항분포로 초기하 분포를 표현할 수 있는지 알아보도록 하겠습니다.
이 과정에서 이 분포에 대한 이해도가 더 깊어질 것이라 확신해요.
(전 항상 확신합니다.)
그럼 시작해보자구요.
다음 문제를 풀어봄으로써, 우리의 주제를 탐구해봅시다.

성공 확률이 p인 베르누이 분포를 따르는 변수가 X_1, ..., X_N개까지
총 N개 있습니다.
서로 독립적인 베르누이의 합이 바로 이항분포이죠.
따라서 우리가 다뤄야 하는
( X1 + ...+ XD | X1 + ... + XN = n)
위 내용은 두 이항분포가 조건부로 겹쳐진 상황이라고 볼 수 있을 것 같네요.
지금 너무 많은 변수들이 들어와 있어 복잡해보이니,
Y= X1 + ...+ XD
Z= X1 + ... + XN
∴ ( Y | Z=n )
이렇게 조건부 분포로 정리하면 더 직관적일까요?
그럼 이제 이항분포로 표현된 위 분포가
초기하 분포를 따른다는 것을 증명하면 문제를 풀 수 있겠어요.
그럼 우리의 전략을 살펴봅시다.
X가 초기하 분포 H(n ; N, D)를 따른다고 할 때,
임의의 x에 대한 확률이 초기하 분포의 확률 형태와 같다면
아까 위 이상한(?) 조건부 분포가 초기하 분포를 따른다고 할 수 있겠죠.
좋아요, 이게 우리의 방향입니다.

그런데 애초에 저런 문제가 왜 책에 있을까요?
해당 분포가 초기하 분포를 따르니까 그런 문제를 냈겠죠?
제 짧은 인생 동안 이런 걸로 장난치는 책은 본 적이 없습니다.
그럼 우리는
직접 수식으로 들어가기 전에
'정답이라고 치고'
직관적인 이해부터 해봅시다.
이항분포의 저 형태가 왜 초기하 분포가 되어야 하는지.
수식으로 증명하는 것은 그 다음에 해도 늦지 않을 겁니다.
좋아요,
일단 베르누이 분포를 따르는 변수가, 그것도 N개나,
아주 근본없게 늘어져 있는 모습이 상당히 심란합니다.
그래서 상황을 조금 정리해보았습니다.
Xk (k=1,2,...,N)들은 베르누이 분포를 따르니까 결괏값이 1 아니면 0입니다.
뭣도 아닌 놈들입니다.
자신감을 가지고,
조건부 분포 정의에 따라 그대로 해석을 해보면
( X1 + ...+ XD = x | X1 + ... + XN = n)
▶ X1+...+XN = n : N개 중 n개가 1이 되었다.
▶ X1+...+XD = x : D개 중 x개가 1이 되었다.
▶ 전체 해석 :
"N개 중 n개가 1이 될 때, D개 중 x개가 1이 되었다"
가만히 보니, 초기하 분포의 정의와 비슷합니다.
"N개 중 n개를 뽑을 때, D개 중에 그 n 안에 포함된 '1' 공의 수"
좋아요,
X1,...,XD
얘네를 '1'이 적힌 공들
이렇게 합시다.
D개 있으니 '1'이 적힌 공의 수 D개와 같으니까요.
그럼
X(D+1), ..., XN
얘네는 N개 중에 D개를 뺀 나머지이니까
'0'이 적힌 공이 되겠네요.
아래 그림과 같습니다.
이제 진한 파란색은 '1'공들
연한 파란색은 '0' 공들이라고
자신의 눈을 속이며 보시면 될 것 같습니다.
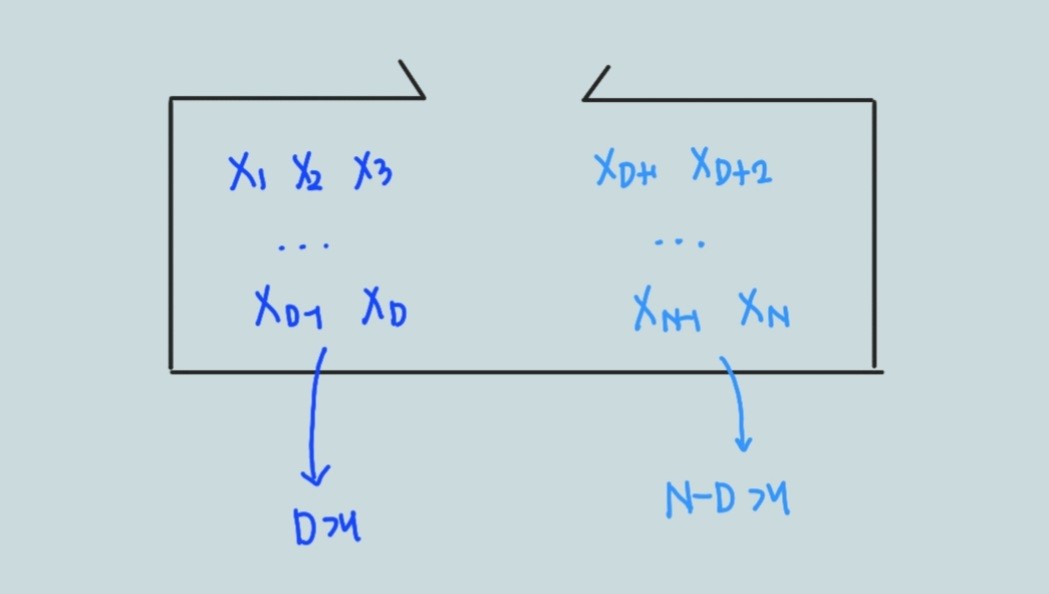
1이 적힌 공 중 X3을 임의로 잡아왔습니다.
이 자식은 X1~XD 사이에 있는 애니까
'1'이 적힌 공이네요.
얘는 베르누이 분포를 따릅니다. 따라서 값이 0 아니면 1입니다.
1이 될 확률은 p이겠구요.
(p가 얼마인지는 사실 상관없습니다.)
그래서 X3이 1값을 가지면
n개 뽑을 때 "뽑혔다"고 보는 것이구요,
반대로 0을 가지면 n개 무작위로 뽑을 때, 손에 걸리지 않았다고 보면 되겠습니다.
(아래 그림에서 X3 자리는 뽑혀 나갔으므로, 이 녀석은 1의 값을 가졌겠군요.)
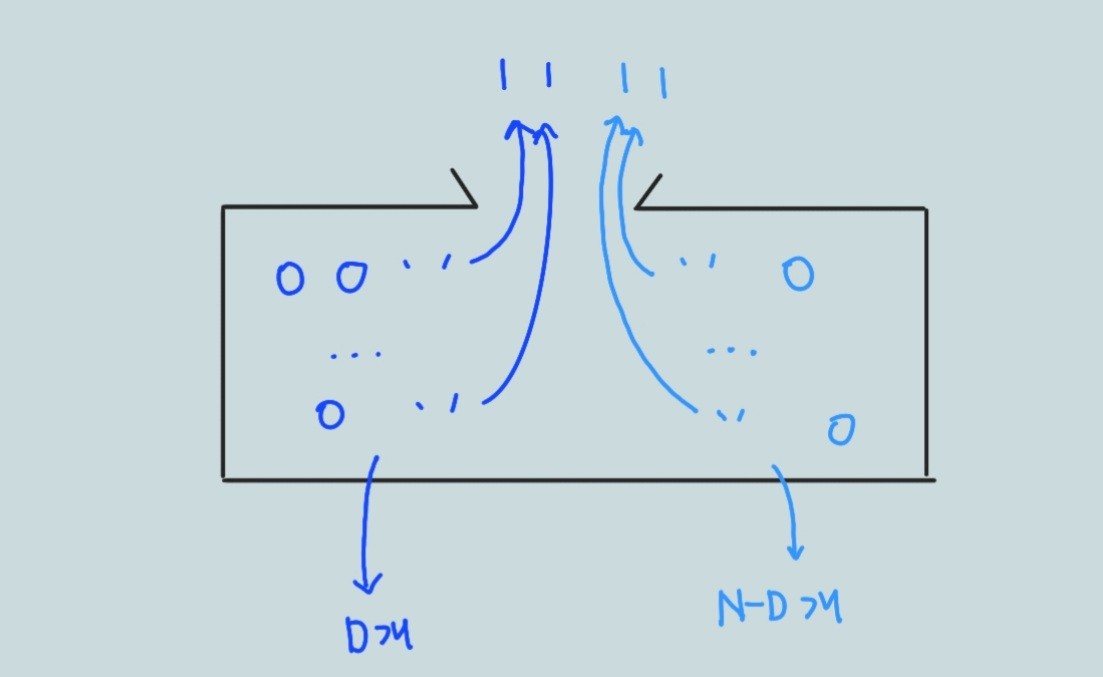
그래서 나중에 운명이 결정되고 나서
다 모아놓고 최종적인 값을 확인했습니다.
X1+...+XD=2
이 뜻은 D개의 '1' 공 중에 단 2개만 뽑혔다는 의미가 되겠네요.
그럼 나머지 '1'이 n개 중 2개 자리밖에 가져가지 못했으니
n개에 뽑힌 나머지 n-2개는 모두 '0' 구슬들(X(D+1), ..., XN) 안에서 나왔겠군요.

바로 위에 적힌 것이
우리가 증명하려고 하던 모습이었습니다.
어떤가요?
아까보단 조금 친숙해졌습니다.
좋아요, 이제 형태의 이유를 이해했으니
한 번 수식적인 증명을 해봅시다.

조건부 분포의 정의에 따라
위와 같이 분모, 분자를 나누어주었습니다.
(별표1)
: (X1+...+XD)는 (X1+...+XN) 안에 들어가 있습니다.
(X1+...+XD = x), (X1+...+XN = n)
그래서 사실 두 경우가 동시에 발생하는 상황은
(X1+...+XD = x)와 (X(D+1)+...+XN = n-x)
이 둘이 동시에 발생하는 상황과 같습니다.
그럼 다음으로 넘어가보죠.

(별표2)
: 문제를 다시 읽어보면, X1, ..., XN은 모두 '독립적'이라고 적혀있습니다.
(X1+...+XD)와 (X(D+1)+...+XN)는 모두 독립적인 애들을 그냥 엉기설기 더해서 합쳐놓은 것이기 때문에
이 둘도 서로 독립적입니다.
그래서
P(A∩B)= P(A)×P(B)
독립성 조건을 여기에 적용해 표현할 수 있었습니다.
(별표3)
: 위에서 잠깐 언급했는데, 우리는 베르누이 분포에서 '성공 확률' p을 굳이 신경쓰지 않고 있습니다.
(물론 상자 구성을 알고 있으니 마음만 먹으면 구할 수 있지만요.)
그런데도 지금 전개식을 보면, 그것은 전혀 문제가 되지 않습니다.
그냥 분모, 분자에서 상쇄되어 없어지거든요.
(이야, 이게 왜 그래야 하는지 또 궁금해지기 시작하죠. 밑에서 다룹니다.)
그래서 최종적으로, 증명이 완료됩니다.
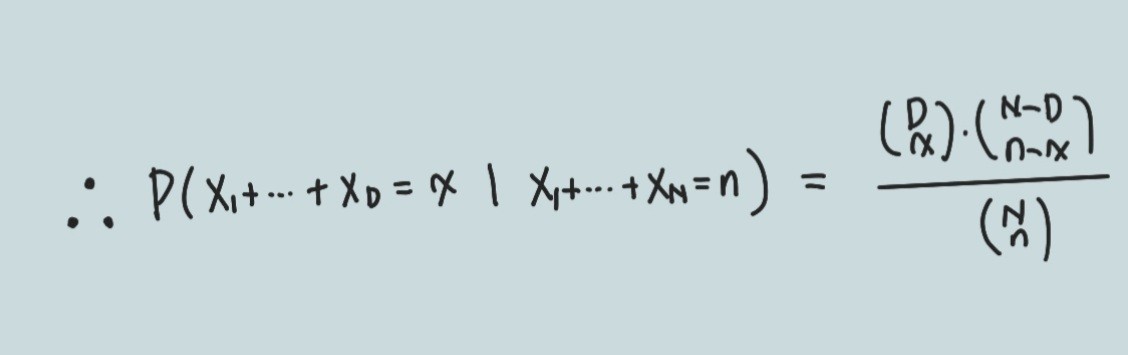
즉, 분포 ( X1 + ...+ XD | X1 + ... + XN = n)는 초기하 분포 H(n; N,D)를 따르는군요.
자, 여기까지 해서 오늘의 주요 기록 내용은 마무리가 되었습니다.
하지만 아직 뭔가 찝찝하죠.
질문)
X1,..., XN는 각각 같은 베르누이 분포 bernoulli(p)를 따른다고 했는데,
또 이항분포의 확률 계산에서 p는 절대적인 역할을 하는데,
왜 p를 활용하지 않아도 초기하 분포 확률 표현이 가능했을까??
이는 제 생각에 우리가 이항분포를 활용한 방식과 관련이 있습니다.
사실 거창하게 베르누이 시행, 이항분포라는 이름으로 부르긴 했지만,
사실 우리가 이 변수들(X1, ..., XN)을 사용한 방식은 단순히
'뽑히면 1, 안 뽑히면 0'
그냥 수식 계산을 하기 위함 '공'을 '변수'로 바꾸어 사용한 정도인 것 같아요.
최종 형태 상으로는 이항분포이니, 이항분포의 확률로 처리하긴 했지만
사실은 그냥 조합(combination)만으로 표현했어도 결과는 같았을 겁니다.
오늘도 함께 해주셔서 감사합니다.
아름다운 느낌이 머물기를...
'수리통계학' 카테고리의 다른 글
| [수리통계학] 11. 이항확률의 포아송 근사 (0) | 2025.02.24 |
|---|---|
| [수리통계학] 10. 포아송 분포와 포아송 과정(Poisson Process) (0) | 2025.02.24 |
| [수리통계학] 8. 이항분포의 기댓값과 분산 계산 (0) | 2025.02.20 |
| [수리통계학] 7. 이항분포란 무엇인가 (1) | 2025.02.19 |
| [수리통계학] 6. E[X(X-1)]의 해석과 초기하 분포의 분산 (1) | 2025.02.17 |