2025. 4. 1. 22:17ㆍ회귀분석
■ 단순회귀모형 회귀계수 추정치 되돌아보기
** 단순회귀모형에서는 편미분을 통해, 상수항(beta0)과 직선의 기울기(beta1)를 각각 계산하였다.
그러나 다중회귀모형에서 회귀계수 추정치를 구할 때는 상수항까지 포함된 행렬, 그 자체를 바로 최적화하였다.
=> 따라서 이 차이가 발생한 지점(상수항을 넣어서 회귀계수를 계산하냐 마냐)을 중점으로 살펴보기로 함.

■ 'No intercept' 모형에서 살펴보는, 상수항과 나머지 회귀계수 간의 관계

* 이렇게 상수항이 애초에 포함되지 않는 모형을 생각해본다고 하자. 이때 독립변수 X는 총 p개로 각 변수는 최적화된 회귀계수(beta1, beta2, beta3, ..., betap)를 가지고 있음.
* 이제 이 모형을 '중심화'시켜볼 것임.

* 이제 이렇게 살펴보면, 1개의 Y와 p개의 X들을 모두 중심화한 식이
결국 상수항(intercept)을 포함한 식이 된다는 것을 확인할 수 있음.
* 다시 말하면,
상수항(beta0)은 나머지 X들의 회귀계수에 변화를 주지 않음.
* 상수항이 나머지 회귀계수들과는 다르게, 꽤나 독립적으로 움직인다는 것을 확인해볼 수 있음.
* 그래서 상수항이 없는 상태에서, beta1, beta2, ..., betap를 구해보도록 함.
■ 상수항을 제외한 회귀계수들만 구해보기
* 먼저 아래와 같이 우리가 계산 과정에 사용할 행렬, 벡터들을 정의하고 감.
* X는 상수항이 포함된, 우리의 원래 독립변수 데이터
* J는 1들로만 이루어진 n×1 열벡터
* X_j는 X에서 상수항만을 뺀 데이터

* 이번에는 Projection 행렬을 정의하고 가겠음.
* 위에서 보았던 1로만 이루어져 있던 J 벡터로 만들 수 있음.

* 이제 준비가 끝났음. 본격적인 계산을 시작해보도록 함.

* 위와 같이 상수항이 없는 회귀계수들을 계산할 수 있음.
* 형태가 익숙하지 않으므로, 아직은 단순회귀모형의 회귀계수와 뭐가 같은지 잘 감이 오지 않으나
* 둘은 형태가 같음.
(* 그림의 마지막 부분은 상수항이 포함된 회귀계수 추정치 형태와 비교)


* (I - P_j)라는 익숙하지 않은 행렬이 끼어 있는데,
결과적으로 말하면 얘가 단순회귀계수와 같이 중심화가 된 회귀계수 추정치를 만들어주는 장치임.
위와 같이
(I - P_j)^2 = (I - P_j)
그래서 하나만 적었던 거임.
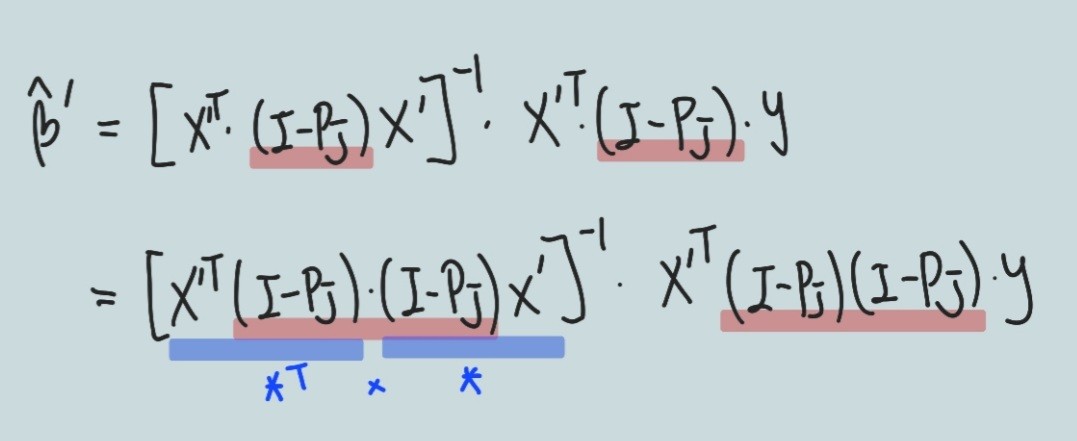
위 * 부분을 밑에서 따로 계산해보면

* 이렇게 (I - Pj)를 이용해 전체 X, Y 데이터에 대해 '중심화'를 했으므로,
위와 같이 중심화된 행렬들로 계산한 회귀계수는 단순선형회귀모형을 공부한 우리에게 익숙한 형태가 된다.
결론
다중회귀모형에서 Y = Xb + e로 상수항을 X에 포함해서 회귀계수를 구할 때,
b = (X^tX)^{-1} (X^tY)와 같이 단순회귀모형의 회귀계수 추정치와 달리 '중심화'가 되지 않은 것처럼 보였다.
하지만 이것은 '상수항을 포함해서' 계산했기 때문이었고,
위에서 다룬 것과 같이, 회귀계수 추정치를 구할 때 상수항을 제거한 상태에서 중심화를 통해 표현하는 방식을 채택했더니, 그 모습이 우리가 익숙한 '중심화를 통한 회귀계수 추정치 (X-Xbar), (Y-Ybar)'가 되는 것을 확인했다.
'회귀분석' 카테고리의 다른 글
| [회귀분석] 14. 표준화된 회귀계수, 베타계수 (0) | 2025.04.03 |
|---|---|
| [회귀분석] 13. 편회귀계수 해석 (0) | 2025.04.02 |
| [회귀분석] 11. 사영행렬(Projection Matrix, or 모자 행렬(Hat matrix)) (0) | 2025.03.31 |
| [회귀분석] 10. 다중선형회귀의 회귀계수 (② 행렬 공간을 이용한 풀이) (0) | 2025.03.30 |
| [기타] X^tAX 꼴 행렬곱 미분 ([회귀분석] 9 포스팅 보충) (0) | 2025.03.29 |